Tutorial: Finding center of rotation from initial and final positions Last edited 4 months ago2024-09-26 14:18:17 UTC
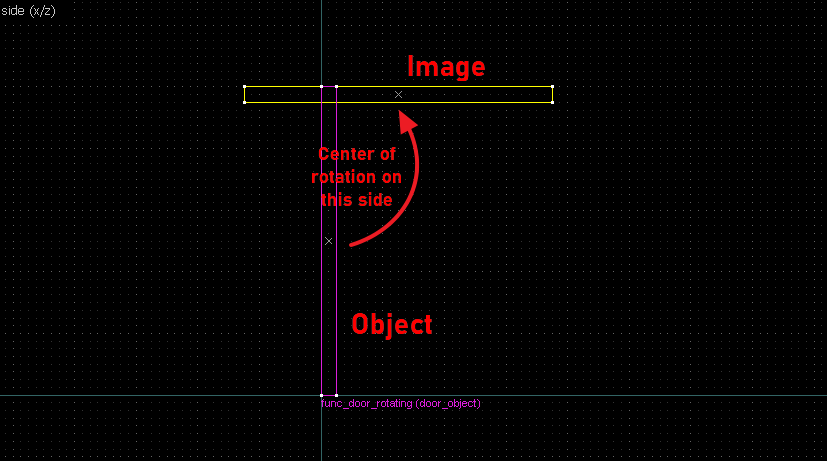
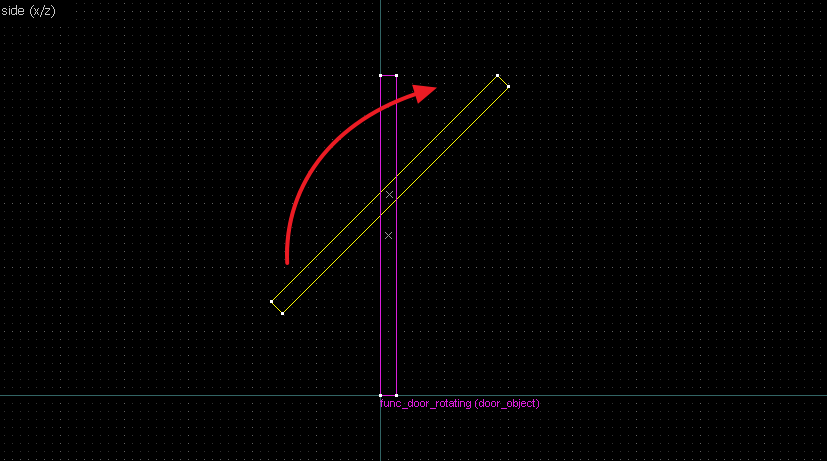
A little lesson in geometrical construction, to find the center of rotation between an object (initial position) and an image (final position). This will help you in building rotating doors that rotate to any final position (or as close to it as J.A.C.K./Hammer allows you).
Throughout this page the terms object (original position) and image (position after rotation) may be used to refer to an entity's initial and final positions, or in case of doors, the closed and open positions.
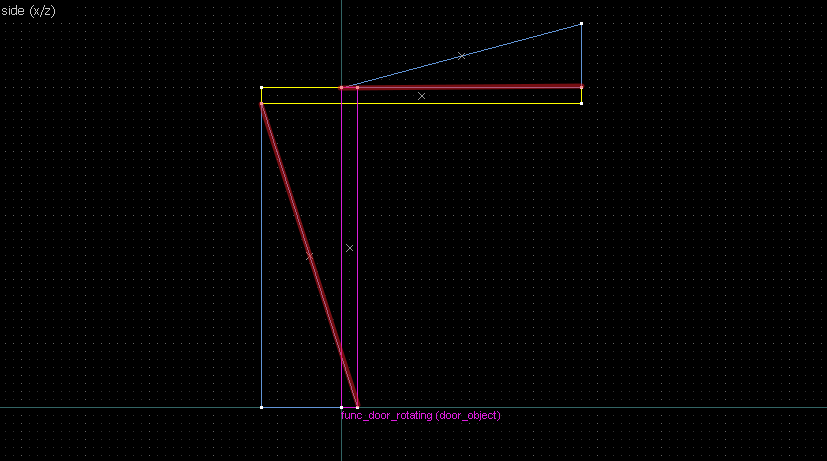
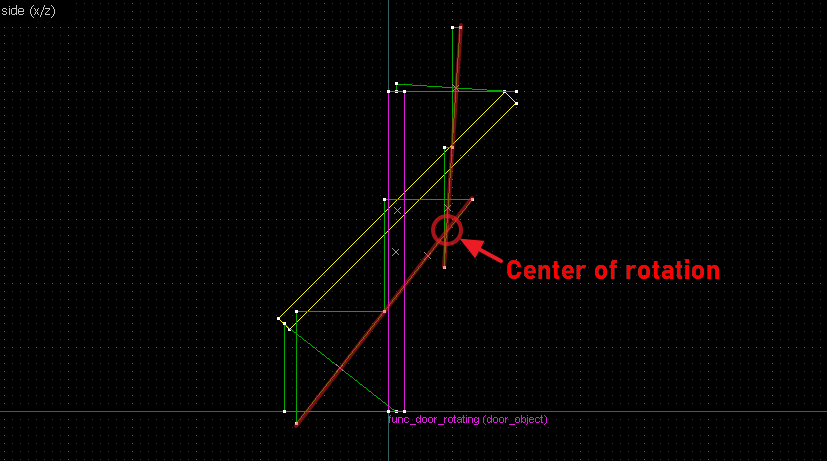
The intersection of the bisectors are our center of rotation. This intersection also happens on grid, but this is not guaranteed for all cases:
Throughout this page the terms object (original position) and image (position after rotation) may be used to refer to an entity's initial and final positions, or in case of doors, the closed and open positions.
Principle
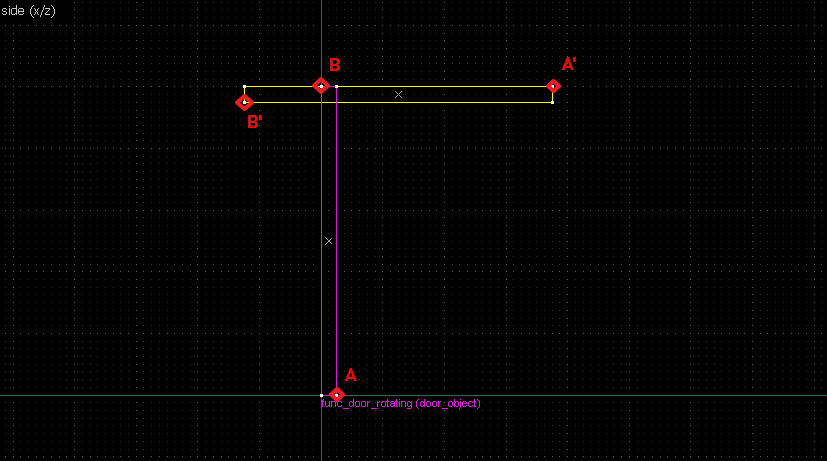
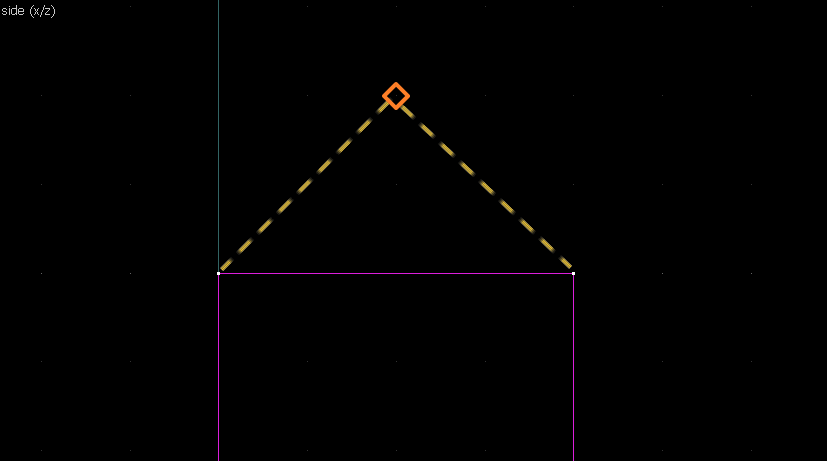
Finding the center of rotation boils down to the following steps:- Identify 2 reference points from an object, and the corresponding points on the image.
- Draw straight lines between the object and image for both points.
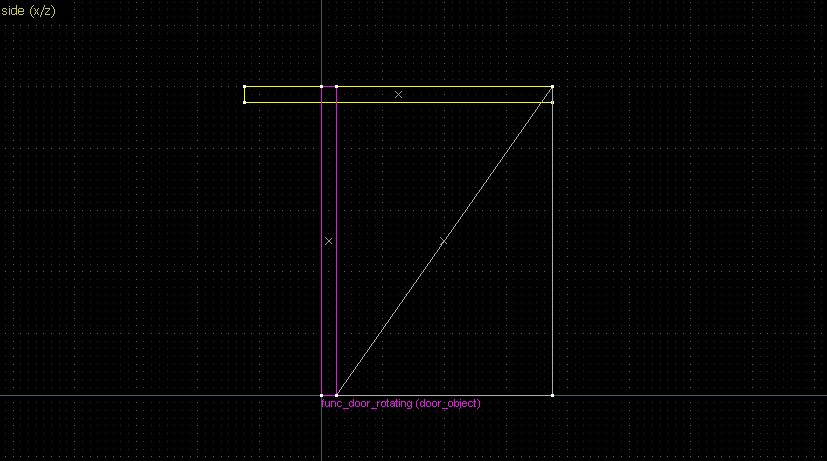
- Draw a perpendicular line for each of the lines at the midpoint (perpendicular bisector).
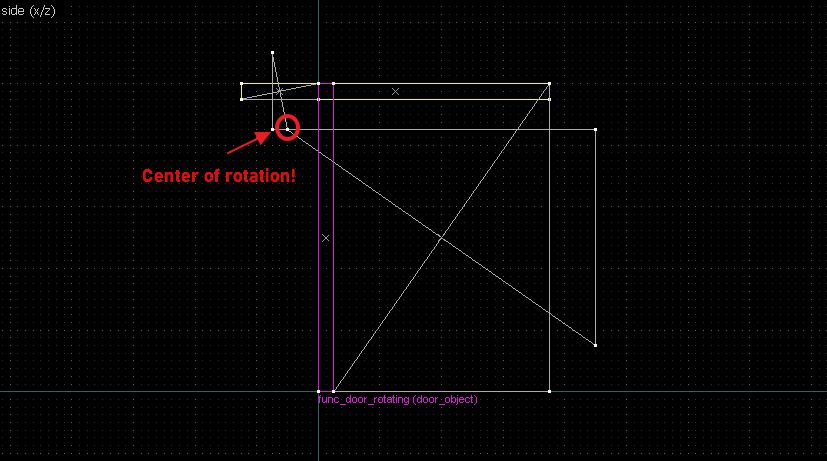
- The intersection of the perpendicular lines is the center of rotation.
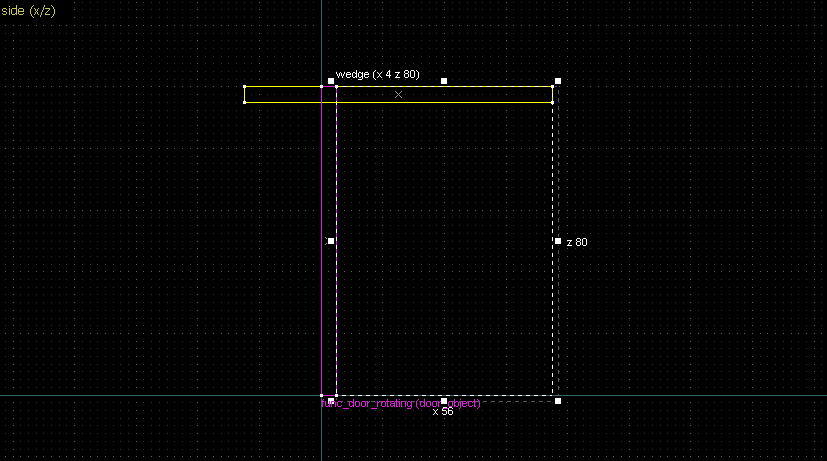
- Drawing a straight line between two points → Wedge primitive.
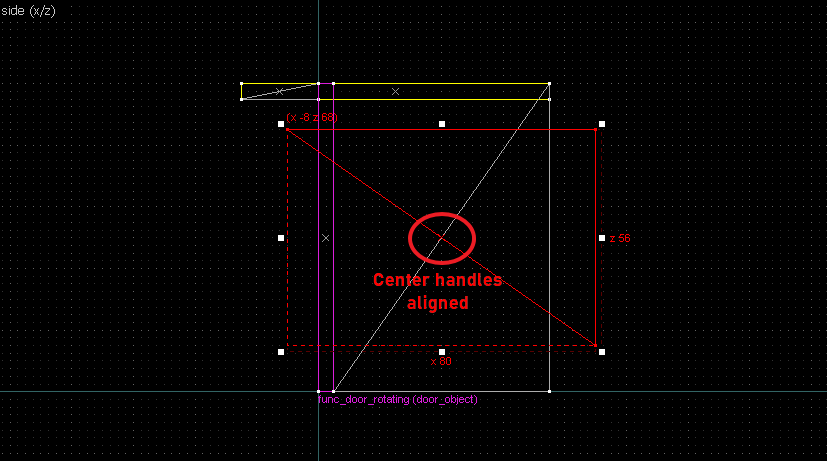
- Drawing a perpendicular bisector → Rotate the wedge 90° and align the center handles.
- Extending a line → Clone the wedge and align the ends.
Examples
1. 90° rotation
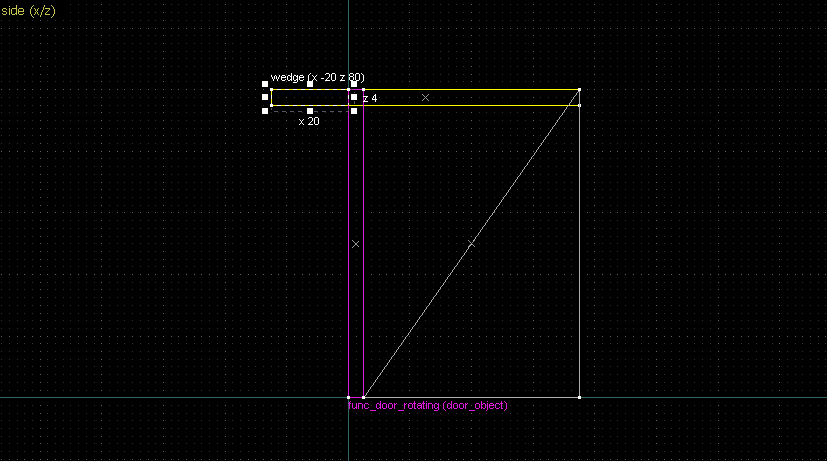
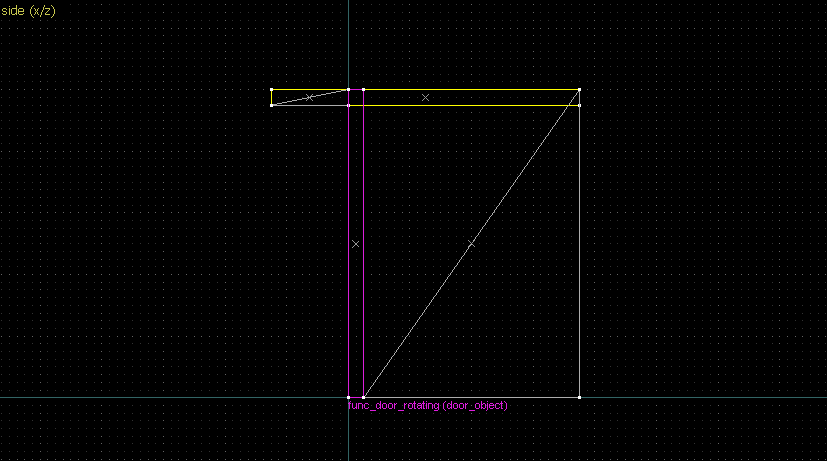
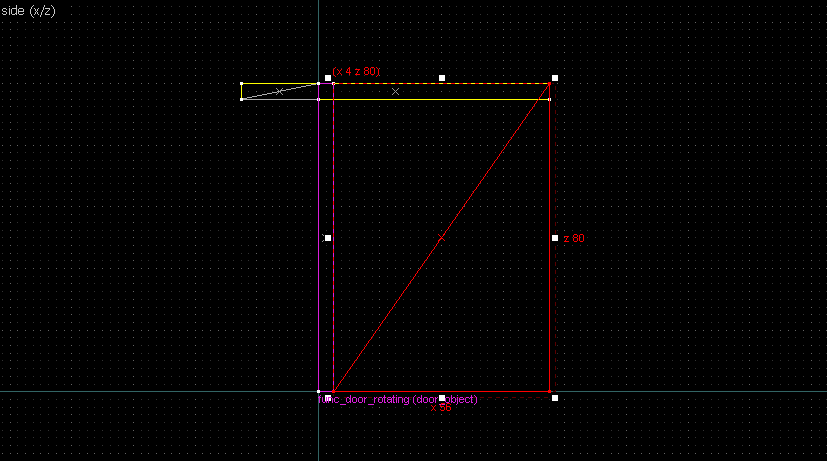
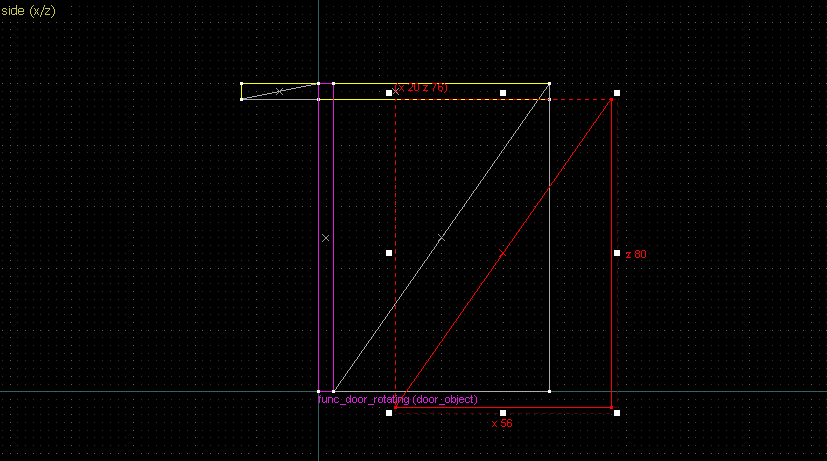
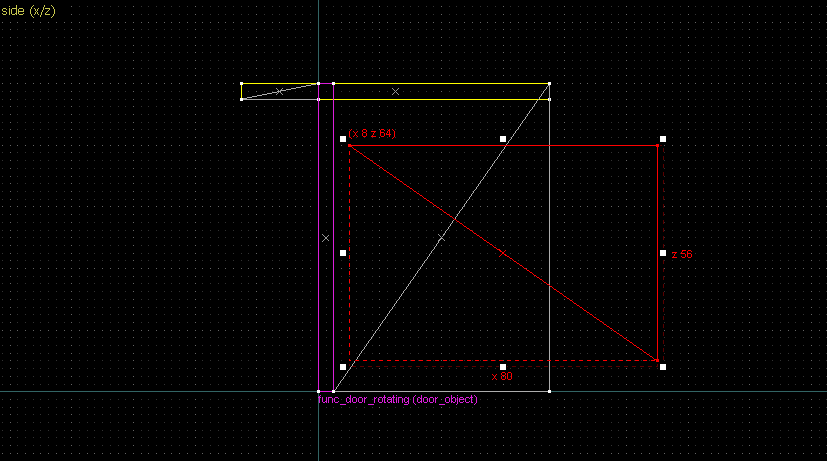
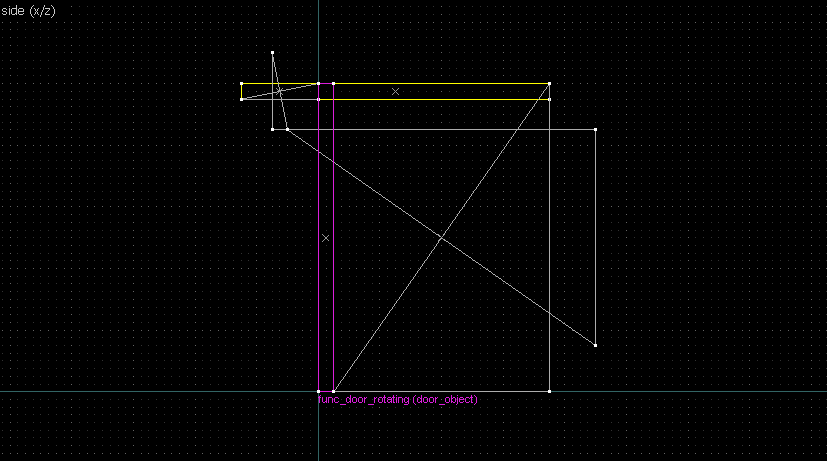
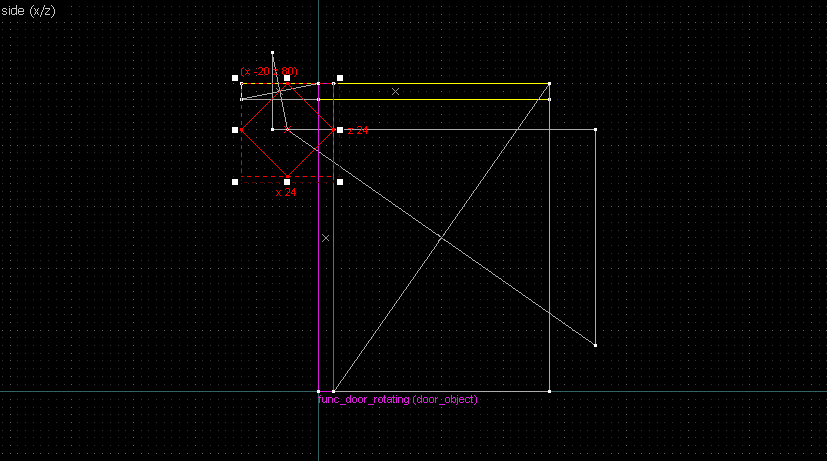
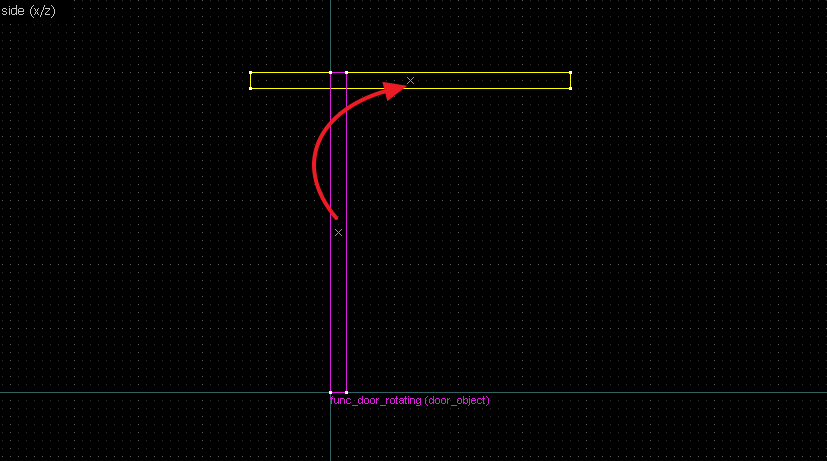
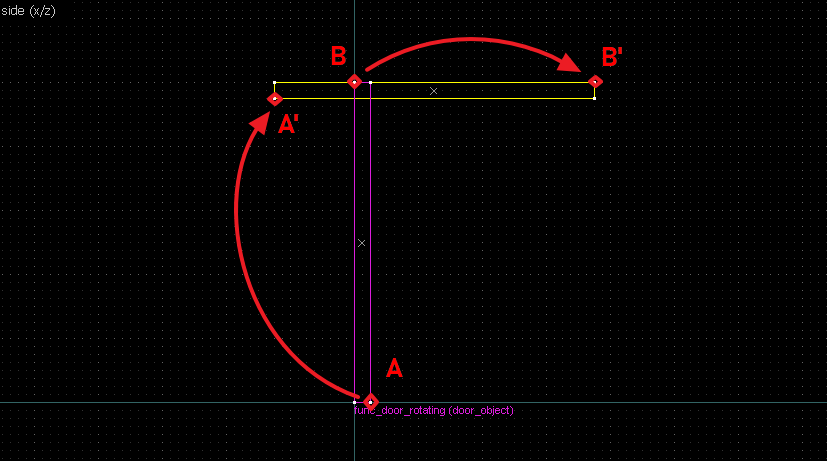
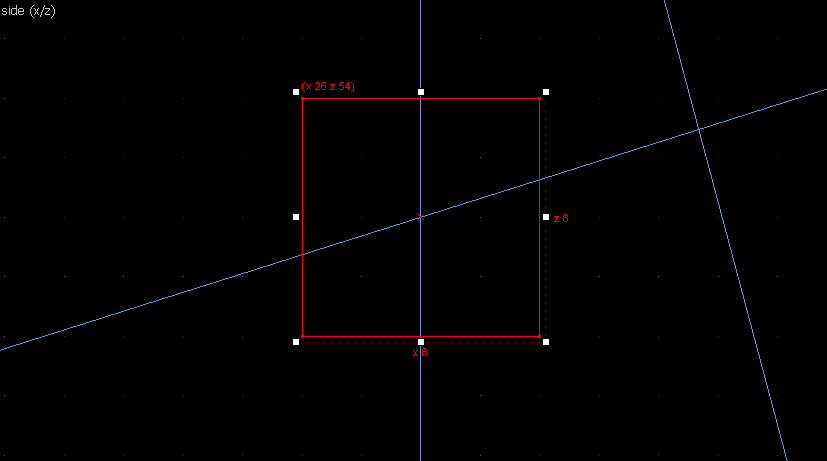
Suppose we want to have following rotation: First we identify 2 points on the object (A and B), and the corresponding points on the rotated image (A' and B'): Now we switch to Block Creation Tool (Shift+B), select the Wedge primitive, and draw a selection that has the object-image point pair at the corners. Then we create the brush. Here's for A-A': And here's for B-B': Now to draw the perpendicular lines. Select the wedge for A-A, clone it, rotate by 90 degrees (direction doesn't matter), and align the center handles (the "x" in the middle of the brush): Now do the same for B-B': And would you look at that! Our perpendicular lines just so happen to intersect precisely to a point on the very first try! That point of intersection is the origin for this rotation! Let's commemorate our success by building our origin brush right there and then!2. 90° rotation (but the other way)
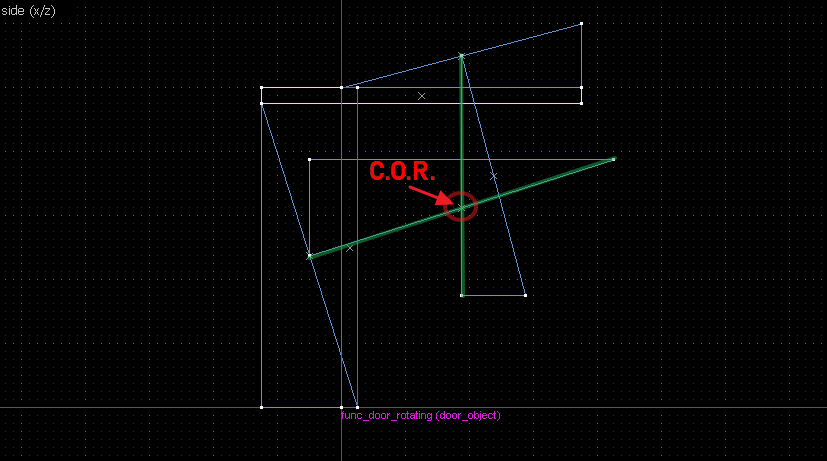
Let's do another 90° rotation, but now it goes the other way: Let's again start by identifying our points: Now we connect the points. Note that B-B' is perfectly horizontal so we'll be using the long straight edge instead of the diagonal edge. Now the perpendicular bisections (in green). Since the "x" handles are on grid this time, I've taken the liberty of aligning the rotated wedges to it directly.The intersection of the bisectors are our center of rotation. This intersection also happens on grid, but this is not guaranteed for all cases:
3. 45° rotation
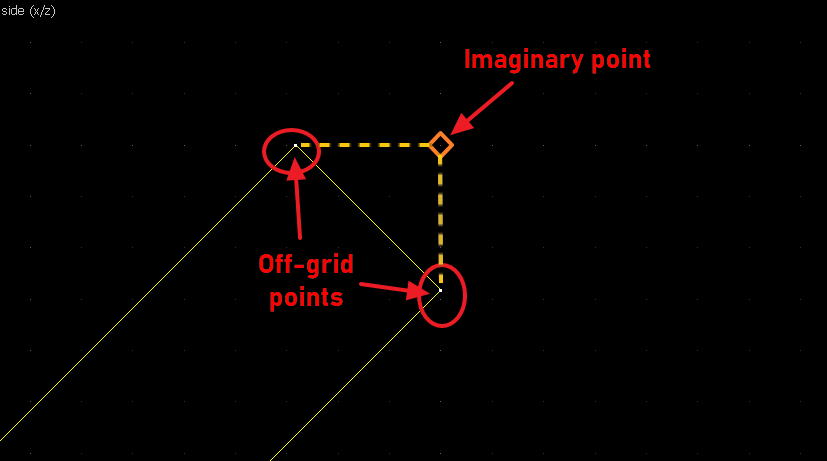
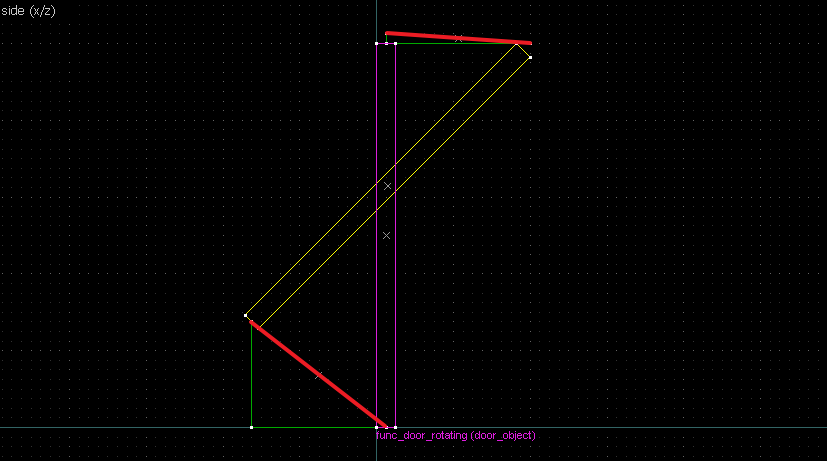
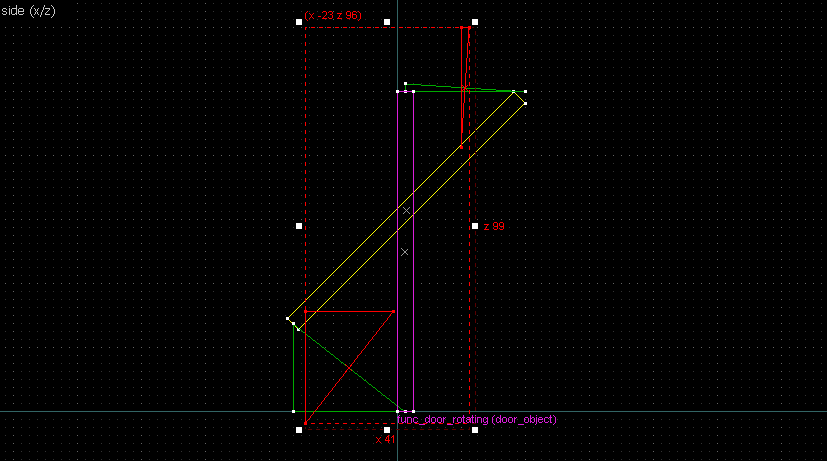
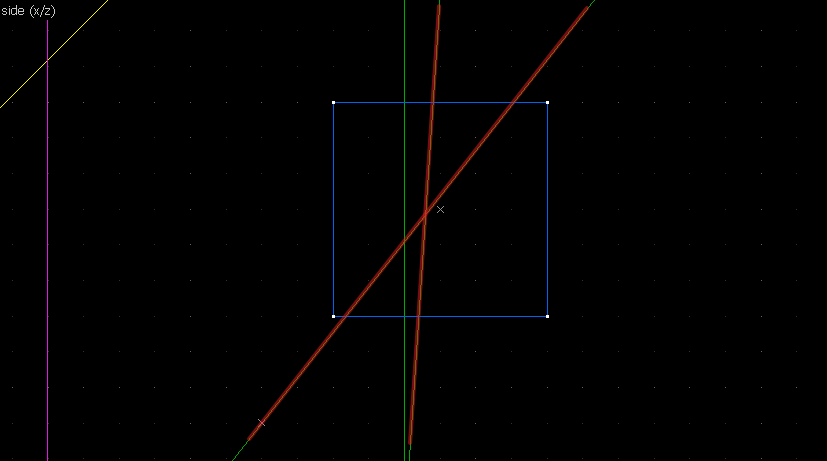
This is going to be a bit more complicated since none of the points on the image are on grid. What we can do instead is to align the whole brush to the top-right side, and imagine there's a point at the corner of the aligning bounds there: And since we know the angles are 45° we can transfer the imaginary point back to the object: As for the other point... none of the points on the other side of the image are on grid too... but the edge line connecting the two has its center very close to be on grid. That'll do. Now we'll do the usual thing. First connect corresponding points (relevant lines in red): Then the perpendicular bisectors (remember: rotate 90° and align the "x" handles): Our bisector lines aren't long enough to intersect, so we'll simply duplicate the wedges and align the ends. Finally, the origin brush. The bisectors (highlighted red) are now intersecting off-grid, so we'll make do with this:Conclusion
Provided the angle of rotation is known beforehand, you'll now be able to place any kind of rotation where the final position would be where you want it to be (or close enough). Hope this helps realize some epic, crazy setups in your minds!- Categories
- Tutorials
- General Tutorials
- Mapping
- Article Credits
-
 kimilil
–
Original author
kimilil
–
Original author
Comments
You must log in to post a comment. You can login or register a new account.