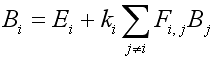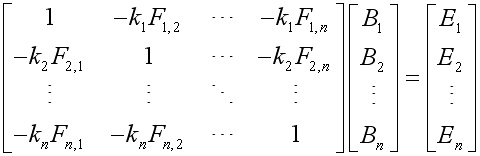VERC: The Inner Workings of RAD Last edited 5 years ago2019-04-16 08:48:46 UTC
You are viewing an older revision of this wiki page. The current revision may be more detailed and up-to-date.
Click here to see the current revision of this page.
It's a common situation: you just want to see what your wonderful creation looks like after tweaking some of the architecture. Happily compiling away, it whizzes through CSG, BSP, and doesn't take too long going through VIS - "great, this won't take long," you think. Unfortunately, the evil demon of RAD likes to take things slowly. Very slowly. 2 hours later, you're still waiting for your level to compile.
Has that been you? Almost certainly - but do you actually know what's going on inside RAD while it seemingly sits there, churning numbers around? If you do, then that's great. However, it's likely that if you're reading this, then you probably don't. This article aims to rectify this situation and put you at your ease - it really is doing something.
Firstly, let's start with the basics. The fourth compile process is named RAD because the lighting process it uses is called radiosity. If you've read the article on photorealism, you'll know that radiosity is a lighting algorithm that belongs to the genre of global illumination. Global illumination means just that - illuminating everything. The non computer scientist may believe, with good reason, that surely every lighting algorithm is of the category global illumination - but this isn't the case.
Rather than simply meaning that everything is lit up some way or another, global illumination refers to lighting things up by properly modeling the interactions between surfaces. Who to the what now? It's like this; imagine a room totally sealed off from any external light sources, with one fluorescant light pointing downwards (which cannot emit light upwards or through the sides at all). If you don't have the light turned on, then the room is pitch black. If you do turn it on, everywhere is illuminated. So what?
Pay particular attention to the fact that I made sure to mention that no light could escape out of the top nor the sides of the fluorescant tube. If you were in this room, however, you'd see the ceiling would be visible - why's that? Surely, if no light can get from the light source to the ceiling - only to the floor and walls - then the ceiling should be pitch black? Well, no. When light hits a surface, some of it is absorbed - but lots of it is reflected back out in all directions, called the diffuse reflectance. Inevitably, as this is reflected out in all directions, light will bounce off the ceiling of the room and get reflected into your eye, thus showing that surface as being illuminated. That's why the ceiling appears to be illuminated - because light bounces off the surfaces, onto the ceiling.
That's what global illumination is about. It's not about taking some magical point that emits light and seeing how far a surface is from it to gauge how much light hits it (Lambertian light model, if you're taking notes) - it's about modeling how light interacts between surfaces, and showing this accordingly.
Having cleared that up, it's time to actually explain the principles of radiosity, and how it works exactly. Let's start by defining the main principle behind radiosity - and it's an important one. Every surface in the scene can absorb light and emit light. It may seem fairly simple, but it has drastic consequences, and forms the base of the radiosity algorithm.
In practice, individual polygons aren't dealt with - smaller surfaces, called 'patches', are used. Every polygon in the scene is split up into small patches, each of which (usually) defines 1 pixel in the end lightmap for the polygon. (This is why lightmaps are low resolution - it'd require thousands more patches and loads more memory to get an accurate high-resolution lightmap.)
Every patch has its own properties (usually inherited from its parent polygon at first). A patch has:
Bpatch = Epatch + kpatch Benvironment
Bpatch is a patch's radiosity, Epatch is its emission, kpatch is its reflectivity (a value between 0 and 1, inclusive) and Benvironment is the incoming light from the environment (the environment's radiosity). A more technical way of expressing it represents it using the light coming in from all the other patches in the environment:Fi,j describes how much light from patch j has reached the patch currently being considered, called the form factor, i (of which ki is the reflectivity, Ei is the emission [if the patch is a light source, this is non zero, otherwise it's zero], and Bi is the actual radiosity of the patch). Bj is the radiosity of patch j currently being examined; but here's where the problem arises. We need to know the radiosities of all the patches to compute their radiosities.
This is where the wonders of matrices arise. I won't go into a discussion as to the ins and outs of how the following would actually be done - this isn't a math article - but I will say that it resolves the problem. A matrix equation can be constructed after a little bit of algebraic manipulation of the above equation, giving:Don't fret; you don't need to know how this works! Suffice to say, it allows the radiosities of all the patches to be found.
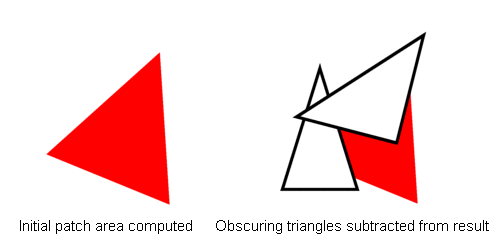
There's one major thing that's been ignored so far, and that's how to compute the form factors - how to find out just how much light from one patch will reach another. There are various methods around, from simply raytracing the scene into memory and seeing how much of each patch is visible, to projecting them onto hemispheres and soforth. One way would be to find the area of the triangle, and subtract any intersecting triangles when projected onto a 2D plane which are between the two patches. It really depends on how accurate the solution needs to be.That's the hardcore computation dealt with. From this, you can see that you'd start off with a scene full of patches that didn't receive any light nor emit any, except for the light sources which would have their emmission cranked up to whatever value it needs to be. The radiosity process would run, and...
Wait! If there's no other light in the scene when the process runs, and the radiosities of all patches are computed in parallel, then how can light reflect back off the surfaces into previously dark areas? Answer: it can't. At least, not until you run another pass of the radiosity algorithm.
This is the whole essence of it, and is where trade-offs occur between realism and speed. It's extremely slow to solve that matrix equation, and gets slower with the number of patches in the scene. Granted, there are optimizations available to the intrepid programmer, but still - most of it is sheer brute force. So, you need to make a decision. Should you run the process 16 times to get a very realistic result, but wait a very long time, or just run it 3 times to get a satisfactory result at the expense of a realistic scene?
That's what the -bounce parameter to the RAD program does - it defines how many times the radiosity process is actually run for the scene. For Half-Life maps, a value of between 2 and 4 gives nice results; after that, things become too 'normally' lit to feel atmospheric (which is what real life is like - your living room isn't in the bowels of hell, is it?).
And thus ends our tour of the RAD program and, more specifically, the radiosity global illumination algorithm. My reference material for this article came from about two pages in "3D Graphics Programming: Games and Beyond" (Sergei Savchenko, Sams Publishing), but I first learnt of this technique out on the big wide world of the web. Get googling!
Has that been you? Almost certainly - but do you actually know what's going on inside RAD while it seemingly sits there, churning numbers around? If you do, then that's great. However, it's likely that if you're reading this, then you probably don't. This article aims to rectify this situation and put you at your ease - it really is doing something.
Firstly, let's start with the basics. The fourth compile process is named RAD because the lighting process it uses is called radiosity. If you've read the article on photorealism, you'll know that radiosity is a lighting algorithm that belongs to the genre of global illumination. Global illumination means just that - illuminating everything. The non computer scientist may believe, with good reason, that surely every lighting algorithm is of the category global illumination - but this isn't the case.
Rather than simply meaning that everything is lit up some way or another, global illumination refers to lighting things up by properly modeling the interactions between surfaces. Who to the what now? It's like this; imagine a room totally sealed off from any external light sources, with one fluorescant light pointing downwards (which cannot emit light upwards or through the sides at all). If you don't have the light turned on, then the room is pitch black. If you do turn it on, everywhere is illuminated. So what?
Pay particular attention to the fact that I made sure to mention that no light could escape out of the top nor the sides of the fluorescant tube. If you were in this room, however, you'd see the ceiling would be visible - why's that? Surely, if no light can get from the light source to the ceiling - only to the floor and walls - then the ceiling should be pitch black? Well, no. When light hits a surface, some of it is absorbed - but lots of it is reflected back out in all directions, called the diffuse reflectance. Inevitably, as this is reflected out in all directions, light will bounce off the ceiling of the room and get reflected into your eye, thus showing that surface as being illuminated. That's why the ceiling appears to be illuminated - because light bounces off the surfaces, onto the ceiling.
That's what global illumination is about. It's not about taking some magical point that emits light and seeing how far a surface is from it to gauge how much light hits it (Lambertian light model, if you're taking notes) - it's about modeling how light interacts between surfaces, and showing this accordingly.
Having cleared that up, it's time to actually explain the principles of radiosity, and how it works exactly. Let's start by defining the main principle behind radiosity - and it's an important one. Every surface in the scene can absorb light and emit light. It may seem fairly simple, but it has drastic consequences, and forms the base of the radiosity algorithm.
In practice, individual polygons aren't dealt with - smaller surfaces, called 'patches', are used. Every polygon in the scene is split up into small patches, each of which (usually) defines 1 pixel in the end lightmap for the polygon. (This is why lightmaps are low resolution - it'd require thousands more patches and loads more memory to get an accurate high-resolution lightmap.)
Every patch has its own properties (usually inherited from its parent polygon at first). A patch has:
- A reflectivity
- An emissive quality
Bpatch = Epatch + kpatch Benvironment
Bpatch is a patch's radiosity, Epatch is its emission, kpatch is its reflectivity (a value between 0 and 1, inclusive) and Benvironment is the incoming light from the environment (the environment's radiosity). A more technical way of expressing it represents it using the light coming in from all the other patches in the environment:Fi,j describes how much light from patch j has reached the patch currently being considered, called the form factor, i (of which ki is the reflectivity, Ei is the emission [if the patch is a light source, this is non zero, otherwise it's zero], and Bi is the actual radiosity of the patch). Bj is the radiosity of patch j currently being examined; but here's where the problem arises. We need to know the radiosities of all the patches to compute their radiosities.
This is where the wonders of matrices arise. I won't go into a discussion as to the ins and outs of how the following would actually be done - this isn't a math article - but I will say that it resolves the problem. A matrix equation can be constructed after a little bit of algebraic manipulation of the above equation, giving:Don't fret; you don't need to know how this works! Suffice to say, it allows the radiosities of all the patches to be found.
There's one major thing that's been ignored so far, and that's how to compute the form factors - how to find out just how much light from one patch will reach another. There are various methods around, from simply raytracing the scene into memory and seeing how much of each patch is visible, to projecting them onto hemispheres and soforth. One way would be to find the area of the triangle, and subtract any intersecting triangles when projected onto a 2D plane which are between the two patches. It really depends on how accurate the solution needs to be.That's the hardcore computation dealt with. From this, you can see that you'd start off with a scene full of patches that didn't receive any light nor emit any, except for the light sources which would have their emmission cranked up to whatever value it needs to be. The radiosity process would run, and...
Wait! If there's no other light in the scene when the process runs, and the radiosities of all patches are computed in parallel, then how can light reflect back off the surfaces into previously dark areas? Answer: it can't. At least, not until you run another pass of the radiosity algorithm.
This is the whole essence of it, and is where trade-offs occur between realism and speed. It's extremely slow to solve that matrix equation, and gets slower with the number of patches in the scene. Granted, there are optimizations available to the intrepid programmer, but still - most of it is sheer brute force. So, you need to make a decision. Should you run the process 16 times to get a very realistic result, but wait a very long time, or just run it 3 times to get a satisfactory result at the expense of a realistic scene?
That's what the -bounce parameter to the RAD program does - it defines how many times the radiosity process is actually run for the scene. For Half-Life maps, a value of between 2 and 4 gives nice results; after that, things become too 'normally' lit to feel atmospheric (which is what real life is like - your living room isn't in the bowels of hell, is it?).
And thus ends our tour of the RAD program and, more specifically, the radiosity global illumination algorithm. My reference material for this article came from about two pages in "3D Graphics Programming: Games and Beyond" (Sergei Savchenko, Sams Publishing), but I first learnt of this technique out on the big wide world of the web. Get googling!
Comments
You must log in to post a comment. You can login or register a new account.