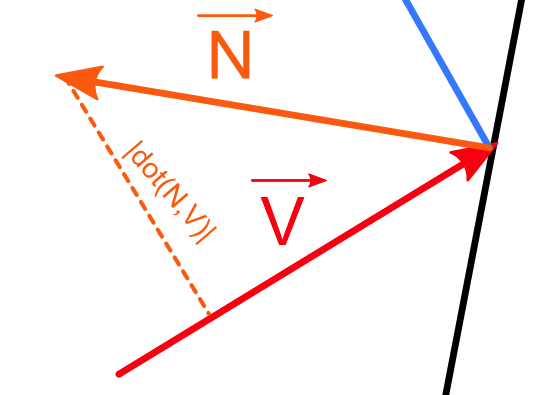
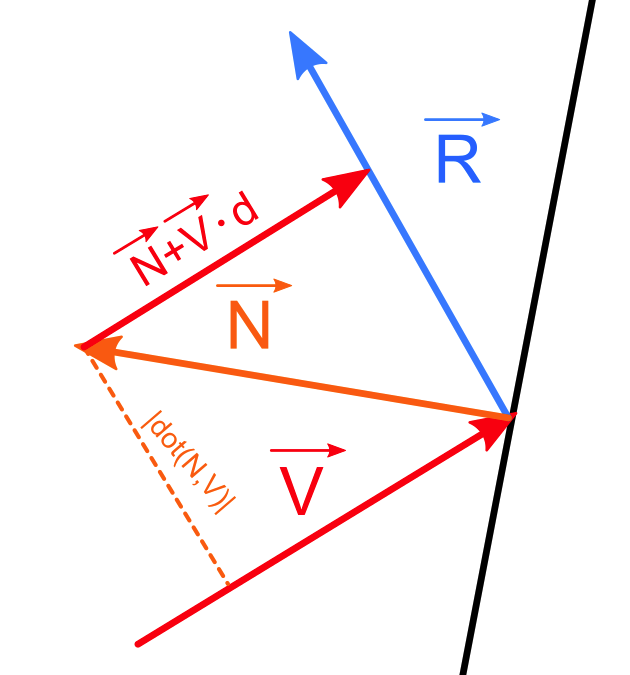
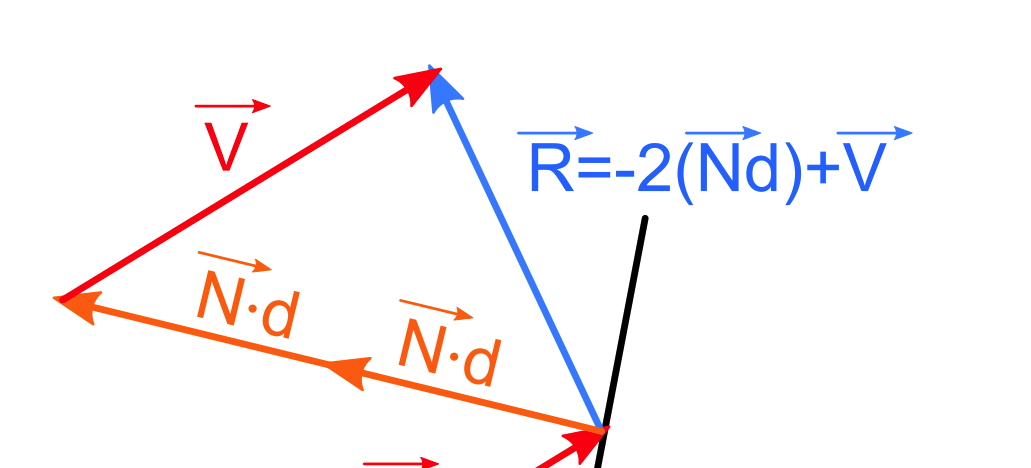
1. Get normalized beam vector and normalized hit plane normal vector.
2. Find first orthogonal vector from cross product between beam vector and plane normal vector. This one represents z-axis in the new vector basis while plane normal vector represents x-axis in the new vector basis. Find second orthogonal vector from cross product between first orthogonal vector and the plane normal vector. This new vector represents y-axis in the new vector basis.
3. Create a Change to Basis Matrix from plane normal vector, first orthogonal vector and second orthogonal vector columns, in that order. Also calculate its inverse.
4. Create a composite matrix by multiplying Inverse Change to Basis Matrix, X-axis Mirror Transformation Matrix(mirroring a beam vector in regards to plane normal vector) and Change to Basis Matrix, in that order.
5. Transform beam vector with calculated transformation matrix. A new vector should be a reflected vector.
While testing, i found out it does properly reflect in certain situations, but it does not i others. What i understood is that it never reflects correctly when neither of new basis vectors is perpendicular to either of the global basis vectors (1,0,0), (0,1,0), (0,0,1). However, if one of the new basis vectors is perpendicular to a certain global basis vector, it might reflect correctly. I checked my matrix methods (inverse, multiplication...) and they all work correctly. I also tried a formula that rotates a vector around another vector, but that also does not work. So i am stuck.
void CTripmineGrenade::ReflectBeam(const Vector& vecStart, Vector beamDir, Vector planeNormal, Vector playerPos)
{
Vector vecOrthoX = planeNormal.Normalize();
Vector vecOrthoZ = CrossProduct(-beamDir.Normalize(), vecOrthoX).Normalize();
Vector vecOrthoY = CrossProduct(vecOrthoZ, vecOrthoX).Normalize();
float* changeToBasis = VectorsToMatrix(vecOrthoX, vecOrthoY, vecOrthoZ);
float* inverted_changeToBasis = InvertMatrix(changeToBasis);
float* transformMatrix = MultiplyMatrix(MultiplyMatrix(inverted_changeToBasis, GetX_AxisMirrorMatrix()), changeToBasis);
Vector newVecDir = TransformVector(-beamDir.Normalize(), transformMatrix);
Vector test_end = RotateVectorAroundAxisVector(-beamDir.Normalize(), vecOrthoZ, GetAngleBetweenVectors(-beamDir.Normalize(), vecOrthoX) * 2);
m_pReflectedBeam = CBeam::BeamCreate(g_pModelNameLaser2, 10);
m_pReflectedBeam->PointsInit(vecStart, vecStart + test_end * 256);
}