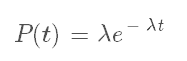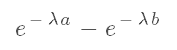VERC: Simulating Randomness Last edited 2 months ago2024-09-10 18:10:24 UTC

Introduction

The current methods employed by most mod authors to simulate random events are very ad hoc and uncontrollable. What this means is that they don't model any real-world distributions, and there is no way of specifying on a long-run basis the average number of times a event should occur per unit time. For most authors this isn't a problem. As long as their method results in something that's "random enough" for their purposes, they'll use it. However, sometimes it is necessary to be able to control the randomness of an event from a higher level. For instance, many RPGs utilize probabilities and rates to control when events should occur. In the long-run, it's important for them to be able to specify exactly just how random an event is. Using existing techniques, this isn't possible.

Shortcomings of Current Methods

To illustrate some of the points made above, let's examine a few common techniques used to simulate randomness:

Discrete Extrapolation

if( random->RandomFloat( 0.0f, 1.0f ) >= 0.5f )
{
  // Fire event
}

m_flNextCheck = gpGlobals->curtime + 10.0f;

I named this one "discrete extrapolation" because of how it works. The reasoning here is that if you take a discrete event, and perform this event every so often, then you have effectively modeled the case where an event has a certain probability of happening every period of time. However this isn't the case. This event is hardly random because it only occurs at 10 second intervals, if at all. It's usually the intention of the author that a certain event has a given chance of firing over the course of a period of time. This leads me to my next example:

Hyperactive Events

if( random->RandomFloat( 0.0f, 1.0f ) >= 0.5f )
{
   // Fire event
}

m_flNextCheck = gpGlobals->curtime + 0.1f;

The common misconception is that if you want an event to occur within a given probability, you simply perform this event as often as possible, and in the long-run it will have happened that often. However, what people forget is that when you're dealing with something continuous like time, events happen within a certain probability within a given amount of time ! Thus, if you were to do the above, your event would really have a probability of happening 50% of the time every 0.1 seconds. This means that on average, your event will occur 5 times every second, or 50 times every ten seconds - rather than 5 times every ten seconds, which is what is probably expected.

Spanning Events

// Fire event

float randomNext = random->RandomFloat( 10.0f, 15.0f );
m_flNextCheck = gpGlobals->curtime + randomNext;

The above specifies that the waiting time between events is randomly distributed between 10 and 15 seconds. That's great, but... what exactly are the parameters of this event? In other words, what's the probability this event happens every 10 seconds? 15 seconds? What's the average frequency of this event in the long-run? While these answers certainly exist, you wouldn't be able to determine them without the help of more advanced statistical model. Thus it follows that without these complex models, you won't be able to condition the values to what they need to be.

The Poisson Arrival Process

The solution to these problems is to use what is known as a poisson arrival process. It is an accurate statistical model for events that occur randomly in a period of time. Without going in to too much detail involving the exact statistics behind this model, given a parameter λ (the rate) that determines the average frequency of the events in the long-run, we can randomly generate the events in such a way that they adhere to this average rate as time goes to infinity. This allows mod authors to have exact control over the randomness of their events over a long-term period of time.

Generation of Events

Our goal is to generate the events in such that they follow the above model. Thus it is important to know that the waiting time between events follows an exponential distribution. The exponential distribution has the following probability density function: What does this mean exactly? In its current form, it doesn't mean anything. Probability density functions aren't meant to be evaluated directly when working with continuous distributions. Instead, what we do is integrate the above function between two time values a and b to determine the probability of an event hapening in that span of time: Evaluating this function with a and b will tell us the probability the event will occur between those two times.

The Parameter and Conversions

In order for the distribution to work as planned, we have to make a few assumptions about our parameter, namely what units it's in. The easiest unit would be seconds since that corresponds with the engine's time unit.

What we have to do next is convert our specifications into their effective parameter. For example, if we want an event to happen on average 6 times every minute, this is the same as 6 times every 60 seconds and thus our parameter would be 0.1 (0.1 times per second). On the other hand, let's say we want an event to happen with probability of 30% every two minutes. In the case of a Poisson distribution, we can actually turn our probability directly into a value, 0.3, and use that in our calculations. Thus our parameter would be 0.0025 (0.0025 times per second). The parameter can also be very small, such as in the case when we want an event to occur with a probability of 10% every hour - our parameter would be 2.8e-5. Lastly, if it's the case where we want an event to happen multiple times per second, then that value becomes the parameter directly.

Implementation

We now have all the information we need to implement our random event generator. I'll leave it as an exercise for you to implement this as an entity, however I will point out a few important points that you need to keep in mind:

General Data

There will be two crucial values you must store; the base time of the current interval, and the last time we checked whether or not to generate the event.

Spawning and Activation

When you spawn the entity, you want to remember to grab the current time so you can use that as a base time to check against, as well as use that time as an initial value for when we last checked. The same goes for any function that otherwise activates the entity (TurnOn input for example) and gets it to start generating events.

The Generation Function

This is the function where the event is fired. I would make it a think function that is called rather frequently, if not every frame. What you do is take the time we last checked and subtract out the base time to get a, and take the current time and subtract out the base time to get b. You can then plug those values into the formula to get a probability. Then you can generate a value between 0.0f and 1.0f and check if it's less than or equal to the generated probability. Is so, fire your event and reset your base time. In all cases, make sure to update your last check time. A sample implementation might look like this:

float a = m_flLastCheck - m_flBaseTime;
float b = gpGlobals->curtime - m_flBaseTime;
Assert( a < b );  // Should never happen where b <= a
float thisProb = log(-rate*a) - log(-rate*b);

if( random->RandomFloat( 0.0f, 1.0f ) <= thisProb )
{
   // Fire event
   m_flBaseTime = gpGlobals->curtime;
}

m_flLastCheck = gpGlobals->curtime;

Additional Features

There are several things you can add to the implementation if you so desire. First, you don't have to check every frame if you don't want. You can check every 0.1 seconds, or every 0.5 seconds. The beauty of the distribution is that is adjusts to the relative time intervals (as it's the area under a curve). Thus, the longer between checks, the larger a chance you have of firing the event. Of course, if you set the interval to be too large, then you lose the random "feeling" of the process, because at some point the period between checks becomes noticeable. For example, if you set the interval to 10 seconds, then your even will noticeably fire on intervals of 10 seconds, or multiples of 10 seconds.

Second, you can add a "grace" period for after events are fired. This is a minimum amount of time to wait before firing another event. Use this when your event is something like a sound or animation that takes a certain amount of time to finish before it can be triggered again. Unlike increasing the check time interval, which essential keeps the process from being evaluated for a certain period of time, when implementing a grace period you want to keep evaluating the process as usual. The only different is before you fire the event, you check to see if the grace time has expired. If it has, then you fire the event. Otherwise, do nothing. Note that you still want to update the base time. Remember, all we're changing is whether or not the event gets fired.

Lastly, try to be as flexible as possible when designing the Hammer entity for your mappers. Provide a TurnOn, TurnOff, and Toggle input so that they can control when the entity generates events. Allow them to specify the parameter as either the number of events per period of time, or as a probability of an event occurring within a period of time. Maybe even let them chose their units (seconds, minutes, hours) if the period of time is large.

If you have any other questions regarding the actual implementation of this entity, remember that it's just like any other logical entity in the SDK that thinks, accepts inputs, and triggers outputs. You can use these entities as an outline for your new logical entity.

Closing

I hope this article gave you a good sense of how to generate random events that are controllable on a long-term basis. For many, the existing techniques may be sufficient, but for those who want precise control, this is the way to go.

Additional Reading

If you want to learn more about the models and distributions used in this article, make sure to check out the links provided above, in addition to a few of the following:

Poisson Distribution
Poisson Process
The Poisson Process