VERC: Random Terrain Generation Last edited 1 year ago2022-09-29 07:55:23 UTC

Rolling hills, jutting rocks, steep cliffs, flat plains - the landscape of the world is very varied. It got there by complex processes of erosion, deposition and eruption over billions of years.

Unfortunately, we don't have billions of years to spare on our computers. We want realistic-looking, eye-catching terrain now, without wasting billions of years doing a complete simulation of the Earth's evolution. So, what do we do? We turn to terrain generation algorithms.

There are many different terrain generation algorithms winging their way around the world of computer graphics, some more complex than others, and each one with their own characteristic results. In this article, I'll explore some of the more popular ones (and show some nice little rendered pictures of them implemented) and explain just what makes them tick.

Let me firstly explain how terrains are represented. A landscape can be represented as a grid of points, each one with its own height. The grid is rigid (each point is the same distance from the other in the X and Z axes) and each point has a height (its position in the Y axis), giving a terrain. This grid is represented in what's called a heightmap - simply an image, where each pixel is one element of the grid (one vertex in the terrain). This is what gets generated by each algorithm.

So, without further ado, let's launch into the first algorithm:

Subdivide and Displace/Midpoint Displacement

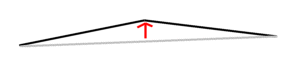
If how fancy the algorithm's name is gives an indication of how good the algorithm is, then this would be absolutely brilliant - and, indeed, it gives great results, being a strongly used algorithm. It works in a fairly simple way, ending up with good results.

To understand this algorithm, it's easier to take a 2D analogy first. Imagine that you have a line (figure 1). You then take the middle of that line and move it up or down by some random amount, giving you two lines at an angle to one another (figure 2). You then do this again to those two lines, giving you four lines (figure 3), then again, and so on. If you keep doing this, you end up with a varied view, containing valleys and hills. This is exactly how the algorithm operates, except on a 2D grid. You start off with one large square. You then split each side in half and raise/lower the midpoints by random values (or, rather, random values scaled down depending on how 'deep' the algorithm has gone - the more squares have been created, the smaller the amount will be, to preserve the features of the landscape generated at the coarser resolutions and give little details at finer resolutions). The midpoints are then connected up with new lines to split the original square into 4 squares. Those two new lines then have the same process applied to them. Then, the process repeats itself, except this time it happens on each of the 4 squares. This keeps happening until the desired resolution of heightmap is generated. And that's it. Pretty simple for a powerful and realistic algorithm.

Fault Formation

No, no, not a segmentation fault. A fault, as in, a fault in the landscape where two tectonic plates meet. You see, this algorithm uses a rather different approach involving shoving great big dirty lines across the landscape, giving a steeply sloping terrain that gives very satisfactory results when a smoothing filter is applied.

You start off with a blank heightmap, every height value at 0. Now, strike a random line across the landscape and raise the terrain on a random side of that line by an amount (figure 4). Keep doing that a number of times, decreasing the amount you add to the heightmap each time (the more you do it, the more detailed and less 'jagged' the terrain will be) (figure 5). Then, a smoothing/blurring filter should be applied (unless you specifically want the jagged effect) such as a FIR filter or a gaussian blur, giving the final result (figure 6).

Perlin Noise

Computer graphics vererans will probably be among the various worshippers of Ken Perlin, the inventor of Perlin noise. Perlin noise is a way of creating a 'random' image that has dark and light areas, rather than just being totally random - perfectly suited to terrain generation. Its operation is rather similar to that of the subdivide and displace algorithm, but it operates on a different basis.

To create a Perlin noise-generated heightmap, you need to add together lots of different heightmaps, some very coarse, some fine, some very fine. The coarsest ones define the basic shape of the landscape, whilst the finest ones define the small details. I won't go into detail with this algorithm, as it can be quite complex, but I'll give a basic overview of how the different heightmaps are constructed.

Basically, at each level, random 'noise' is generated - random numbers are assigned. The coarser the heightmap is, the less numbers are assigned, and the bigger areas that have the same number assigned - the coarsest level would be simply 4 patches, each at a different level. Then, the different numbers are interpolated between using a special interpolation function to get a smooth change from one to the other. This is done at each level, then the resultant heightmaps are all added together to generate the end result.

A much more in-depth and accurate description, with examples, of Perlin noise is available here.

But what do they look like?

It would be unfair of me to simply leave you there, without examples as to what they look like, wouldn't it? Yes, it would, so I'm going to give you examples of the above 3 methods - specifically, a heightmap, and a render of that heightmap in Bryce. (The subdivide and displace and the Perlin noise heightmaps were generated by Terragen, and the fault formation heightmap was generated by my own pet program).

Subdivide and Displace

Fault Formation

Perlin Noise

So, there you have it. There are various other algorithms around (such as particle deposition) which aren't used quite as frequently, but if you're interested, information can be found about them by Googling it.